| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- WTI
- 중국경제
- 테슬라
- 지엔티파마
- FOMC
- prometheus
- 아모레퍼시픽
- WTI유
- 주가분석
- 중국증시
- 유상증자
- 머신러닝
- 퀀트
- 엘론 머스크
- 뉴지스탁
- 국제유가
- 기업분석
- 경제위기
- 뇌졸중
- 넬로넴다즈
- 주식투자
- 마법공식
- 스크리닝
- Python
- 금리인상
- DSP
- 제다큐어
- 반려견치매
- 미국금리
- 코로나19
- Today
- Total
목록Robotics/Theory (4)
Data Analysis for Investment & Control
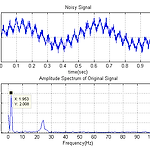 Matlab > FDA Tool을 이용한 FIR 필터 설계
Matlab > FDA Tool을 이용한 FIR 필터 설계
신호처리 시간에 배우는 필터 중에서 활용도가 높은 필터 중에 하나는 FIR 필터이다. 구현이 비교적 간단하다고 알려져 있으며 IIR 필터에 비해 안정성이 높다. 이번 시간에는 Matlab에 내장되어 있는 필터 설계 툴을 사용하여 이 FIR 필터를 설계하는 방법을 알아보도록 하겠다. 노이즈가 포함된 신호 필터 효과를 검증하기 위해 샘플 신호를 생성해 보도록 하겠다. 샘플 신호는 원본 신호에 노이즈를 첨가하여 생성하는데, 원본 신호의 Amplitude는 2, 주파수 역시 2Hz로 선정하였다. 노이즈 신호는 두 가지로 하나는 저주파 노이즈, 다른 하나는 고주파 노이즈를 생성하여 원본 신호에 더해주었다. 다음은 원본 신호와 노이즈 함수를 나타낸다. 여기서 f_n1 = 24Hz, f_n2 = 0.2Hz의 주파수를..
 스미스 예측기(Smith Predictor)를 이용한 시간 지연 제어
스미스 예측기(Smith Predictor)를 이용한 시간 지연 제어
소개 및 수식 유도 스미스 예측기는 시간 지연을 가지는 시스템을 제어하기 위한 예측 제어기로 Otto J. M. Smith라는 사람이 1957년에 발명하였다. 시간 지연을 가지는 Closed-Loop 제어 시스템에서 스미스 예측기를 추가하게 되면 아래와 같은 블록도로 표현할 수 있다. 여기서 C는 제어기의 전달함수이며, G는 플랜트의 전달함수이다. 스미스 예측기는 플랜트 전달함수 G의 추정 식을, 그리고 시간 지연량을 조합하여 피드백하는 방식으로 시간 지연 요소로 기인하는 불안정성을 보상한다. 위의 블록도를 수식화 하면 다음과 같다. 여기서 W에 대해 정리하면, 정리한 W를 위의 식에 대입하면, 즉, 스미스 예측기로 인해 제어의 불확실성 요소는 상쇄되고 시간지연 성분만 남게 된다. 따라서 제어 시스템이 ..
칼만필터(Kalman Filter)는 노이즈가 포함되어 있는 선형 역학 시스템의 상태를 추적하는 필터로 루돌프 칼만이라는 사람에 의해 개발되었다. 칼만필터는 신호처리, 로봇 공학 등의 여러 분야에 사용되며, 매우 효율적인 성능으로 널리 쓰이고 있다. 여기에서는 칼만 필터의 수식 유도 과정에 대해 Gaussian Probability Density Function 관점에서 설명한다. ※ 내용상 잘못된 부분이나 수식 오류 등이 있는 경우에는 지적해 주시면 감사하겠습니다. 2017.05.03 Update
 FIR 필터와 IIR 필터
FIR 필터와 IIR 필터
디지털 필터에는 두 종류가 있는데 하나는 FIR(Finite Impulse Response) 필터이고, 다른 하나는 IIR(Infinite Impulse Response) 필터이다. FIR 필터와 IIR 필터의 구조적인 차이를 보면 다음과 같다. FIR 필터는 출력이 귀환되어지는 것이 없이 입력에 의해서만 출력이 결정된다. z변환을 하면 전달함수를 구하면 다음과 같다. 임펄스 응답을 구하면 다음과 같다. 따라서 다음과 같이 표현된다. IIR 필터는 입력 뿐만 아니라 출력이 귀환되어 진다. z 변환을 하면 다음과 같다. 분모와 분자를 정리하면 다음과 같다. k를 n으로 바꾸고 정리하면 전달함수는 FIR이나 IIR필터를 선택할 경우에는 두 필터의 장점을 고려하여 맞는 필터를 선택한다. 두 필터 사이의 상대적..
